Chapter 2 - Algorithm Discovery and Design

(2.2) Representing Algorithms

(2.2.1) Pseudocode: How should we represent algorithms? What notation should we use so that they are clear, precise, and unambiguous?

A natural language like English, French, or German is a possibility but look at Figure 2.1 in the text.

The opposite extreme is to write algorithms in a formal programming language like Pascal, C++, or Java but take a look at Figure 2.2 which is a fragment of a C++ program for the addition algorithm of Figure 1.2.

A good compromise is pseudocode, a special set of English language constructs modeled to look like most programming languages. It is simple, highly readable, and has virtually no grammatical rules. The algorithms in Figures 1.1 and 1.2 are written in pseudocode.

(2.2.2) Sequential Operations: A sequential operation performs computation, input, or output.

A computation operation computes the value of an arithmetic expression and stores the value in the memory location of a variable:

Some examples are:

An input operation gets the value(s) for one or more variables from the outside world:

Some examples are:

An output operation sends the value(s) of one or more variables to the outside world:

Some examples are:

An output operation may also send a message to the output world:

(2.2.3) Conditional and Iterative Operations: A conditional operation contains a true/false condition and two sets of algorithmic operations:

If "true/false condition" then
"first set of algorithmic operations"
Else
"second set of algorithmic operations"

  1. First the "true/false condition" is evaluated to see if it is true or false.

  2. If the condition is true then the "first set of algorithmic operations" is performed and the "second set of algorithmic operations" is skipped.

  3. Otherwise, if the condition is false then the "first set of algorithmic operations" is skipped and the "second set of algorithmic operations" is performed.

  4. In either case, after performing one of the sets of operations, the algorithm proceeds to the step following the conditional operation.

The following diagram is a flow chart that the computing agent follows whenever he/she/it encounters a conditional operation in an algorithm:

An example of a conditional step is:

If (c i > 9) then
Set the value of c i to (c i - 10)
Set the value of carry to 1
Else
Set the value of carry to 0

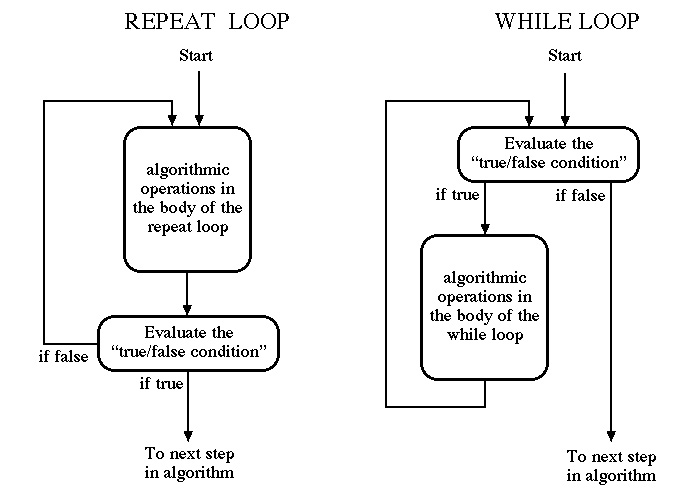
An iterative or looping operation can be written in pseudocode as a repeat loop :

Repeatstep i to step j until "a true/false condition" becomes true
step ioperation
step i +1operation
.
.
.
step joperation

The loop body contains step i through step j and is usually indented. The termination condition is "a true/false condition". A repeat loop performs all the steps in the loop body and then evaluates the termination condition. If the termination condition is false then the repeat loop performs all the steps in the loop body again and then evaluates the termination condition again. This is repeated until the termination condition is finally true and the algorithm can proceed to the next step. The loop body of a repeat loop is always performed at least one time.

Here is an example of a repeat loop:

Step 1Set the value of count to 1
Step 2Repeatstep 3 to step 5 until ( count > 100)
Step 3Set square to (count * count )
Step 4Print the values of count and square
Step 5Add 1 to count

Another way to write a loop is to leave out the step numbers and add a line indicating the end of the loop:

Set the value of count to 1
Repeatuntil (count > 100)
Set square to (count * count )
Print the values of count and square
Add 1 to count
End of the loop

The while loop is another kind of iterative operation:

While"a true/false condition" remains true do
operation
.
.
.
operation
End of the loop

Instead of a termination condition that is evaluated after each iteration of the loop body, a while loop has a continuation condition that is evaluated before each iteration of the loop body. If the continuation condition is initially false then the loop body is never executed.

Whenever a computing agent encounters a repeat loop or a while loop in an algorithm he/she/it follows one of the flow charts in the following diagram:

(2.3) Examples of Algorithmic Problem Solving

Here is the pseudo-code for Euclid's algorithm to compute the Greatest-Common-Divisor (GCD) of two positive integers, A and B. This pseudo-code uses subtraction instead of long-division. 

GCD(A, B)
    while (A ≠ B) do
        if( A > B) 
            then 
                Set A to A - B
            else 
                Set B to B - A
        end-if
    end-while
    Set the value of GCD to A

(2.3.2) Example 2: We are given an unalphabetized list of 10,000 names with their telephone numbers:

NameTelephone Number
N1T1
N2T2
N3T3
..
..
..
N10,000T10,000

and we want to find the phone number for a particular person, NAME. If NAME is in the list then the algorithm should print the appropriate phone number, else, it should print a message that the person is not in the list.

Figure 2.11 shows a first attempt at an algorithm for this problem: it is excessively long and inefficient and doesn't print any message if the person is not in the list.

Figure 2.12 shows a shorter, more efficient attempt: it quits searching when it has found the person but it assumes the search will always find the person in the list.

Figure 2.13 shows the final algorithm: the loop terminates when the person is found or the whole list has been searched. It's the best way of searching an unordered list. Chapter 3 will show we can search much faster if the list is sorted (alphabetized.)

(2.3.3) Example 3: We are given an integer, n, that is greater than or equal to 2 and list of n unique numbers, A1, A2 ..., An. The problem is to find and print out the largest value in the list and its location in the list.

Figure 2.14 shows an algorithm for this problem.

(2.3.4) Example 4: We are given some text of n characters, T1, T2 ..., Tn, and a pattern of m characters, P1, P2 ..., Pm, where m is not more than n. The problem is to find and print out every location where the pattern occurs within the text.

This is a common problem in computer science called pattern matching. A word processor solves this problem whenever you ask it to find some pattern in the document you are working on. It also arises whenever a geneticist searches the human genome for a particular pattern of nucleotides.

For example suppose we are searching the text: "to be or not to be, that is the question" for the pattern: "be"

So the algorithm executes two steps repeatedly until the pattern has been shifted across the whole text:
  1. Check to see if every character in the pattern matches the corresponding character in the text.
  2. Shift the pattern one place to the right.

Figure 2.15 is an initial draft of the algorithm.

Figure 2.16 is the final draft.

Before leaving the pattern matching problem we should note that more efficient algorithms, like the KMP-Matcher, exist.

Kenneth E. Batcher - 1/21/2009