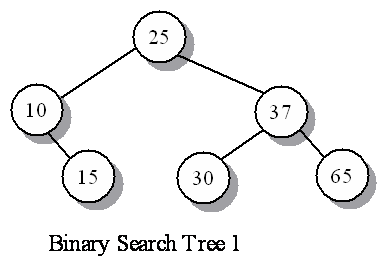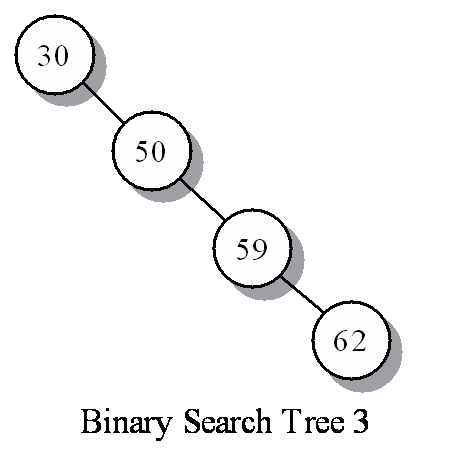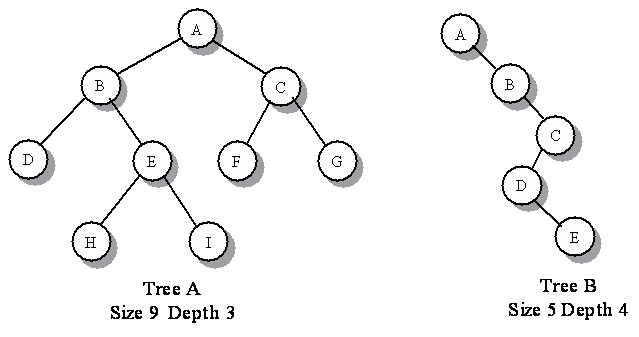
Binary Trees / Binary Search Trees

More Terms

binary tree A binary tree is a tree in which each node has two children, possibly absent, named the left child and the right child.
complete binary tree A complete binary tree is is a binary tree of depth n where all nodes in levels 0 through n - 1 levels inclusive have degree 2 and nodes at level n occupy the leftmost positions in the tree.
full binary tree A full binary tree is a binary tree in which all leaves have the same depth and all internal nodes have degree 2.
balanced binary tree A balanced binary tree is binary tree where the depth of all leaves is the same or 1 plus the least.
degenerate binary tree A degenerate binary tree is a binary tree in which each node has 1 child.

 

 

 

 

 

 

 

Density

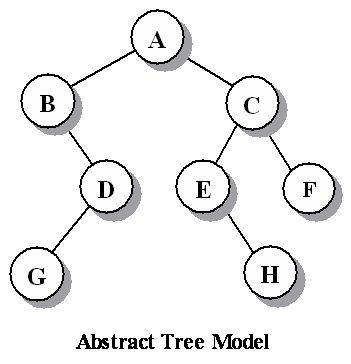
At each level d there may be from 1 to 2d nodes.

level 0:1 to 20= 1 node
level 1:1 to 21= 2 nodes
level 2:1 to 22= 4 nodes
level 3:1 to 23= 8 nodes
etc.

In a full binary tree of height d there will be 2(d + 1) - 1 nodes.

Consider a tree of height 3. 

1 + 2 + 4 + 8 = 15 = 24 - 1

We can recall binary to decimal conversion as a memory aid. Example, convert 1001 to base 10: 

    8  4  2  1
    1  0  0  1two  = 8 + 0 + 0 + 1 = 9
or
    23 22 21 20
    1  0  0  1two  = 23 + 0 + 0 + 20 = 9

Consider, convert 1111 to base 10: 

    8  4  2  1
    1  1  1  1two  = 8 + 4 + 2 + 1 = 15
or
    23 22 21 20
    1  1  1  1two  = 23 + 22 + 21 + 20 = 15

Note: 

 24 23 22 21 20
    1  1  1  1two
+            1two
   -----------
 1  0  0  0  0two =  24 = 16

 10000two = 1111two + 1two

 10000two - 1two = 1111two

So, 

 24  - 1 =  23 + 22 + 21 + 20

And, in general, 

 2(d + 1) - 1 =  2d + 2d - 1 + ... + 21 + 20

In a complete binary tree of height d there will be at least 2d nodes. Levels through d - 1 form a full tree and there is at least 1 node in the next level (at the left).

Using the above formula, in the complete part of the tree there are:
2[(d - 1) + 1] - 1 = 2d - 1
nodes. Adding one more we get:
2d - 1 + 1 = 2d

Thus in a complete binary tree the number of nodes, n is: 

2d <= n <= 2(d + 1) - 1 < 2(d + 1)
or
 2d <= n < 2(d + 1)

Given the number of nodes, what is the depth of a complete binary tree? 

    log2(2d) <= log2(number of nodes) < log2(2(d + 1))
    d <= log2(n) < d + 1

Since the depth must be a whole number we get the following, where n is the number of nodes and int() means discard the fractional part.

Depth of a complete binary tree: 

    d = int(log2(n))

Consider a complete binary tree that has 15 nodes. (Draw it and compute d = int(log2(n))).

For a full binary tree, with n nodes and height h,