Binary Search Trees

A binary search tree has the property, for any node x be a node in a binary search tree,

if node x is in the left subtree of node y, then x's value < y's value
if node x is in the right subtree of node y, then x's value > y's value

        30
       /  \
     15    40
    /  \   / \
   9  18  38  44
   /   /  / \
  5   17 31 39
  /
 1

For a BST an inorder traversal outputs the nodes in order.

We look at pseudocode for BST common operations.

Search

Binary search tree search, recursive.

bstSearch(n, v)           // node n, value v
    if (n == 0 || v == n->value)   // not in tree or n has the target 
        return n
    else if (v < n->value)      // search left subtree
        return bstSearch(n->left, v)
    else if (v > n->value)      // search right subtree
        return bstSearch(n->right, v)

Binary search tree search, iterative.

bstSearch(n, v)           // node n, value v
    while (n != 0 && v != n->value)
        if (v < n->value)
            n = n->left       // search left subtree
        if (v > n->value)
            n = n->right       // search right subtree
    endwhile
    return n

Current Node Action -LOCATING DATA IN A TREE-

Root = 50 Compare item = 37 and 50

37 < 50, move to the left subtree

Node = 30 Compare item = 37 and 30

37 > 30, move to the right subtree

Node = 35 Compare item = 37 and 35

37 > 35, move to the right subtree

Node = 37 Compare item = 37 and 37. Item found.

Minimum

Binary search tree minimum. The leftmost child has the minimum value.

bstMin(n)           // node n
    while (n->left != 0)
        n = n->left
    endwhile
    return n

What change is needed for maximum?

Insert

Binary search tree insertion. If the tree is not null make the new node the root, otherwise search for leaf location where inserting a new node will maintain the BST property.

bstInsertion(T, n)      // T is a tree, n is a node
    root = T.root
    if (root == 0)      // empty tree
        T.set_root(n)
    else
            // Do a binary search to find where node should go. Keep
            // track of each node's parent as we go down through the tree.
        x = root
        while (x != 0)    // there is at least 1 iteration
            par_x = x     // save parent of x
            if (n->value < x->value)
                x = x->left  // move to left subtree
            else
                x = x->right // move to right subtree
            endif
        endwhile

            // Do insert, x is null, par_x is parent of x
        if (n->value < par_x->value)
            par_x->left = n
        else
            par_x->right = n

The resulting tree is not necessarily balanced.

Create the binary tree that results from inserting the following sequences of values (in the given order):

10, 7, 12, 5, 22, 4, 6, 25, 21
10, 11, 13, 17, 22, 25

Successor

Binary search tree successor. Think of the inorder traversal. Two cases:

node n has a right child -
The successor of n is the minimum of n's right subtree.
node n doesn't have a right child -
Move up parent links as long as each node is its parent's right child. When a node is the left child of its parent, the parent of that node is the successor of node n.

Or, find the subtree of which n is the maximum, the parent of the root of that subtree is n's successor.

Requires a parent link.

Ex., Given the tree below find: successor(8), successor(22), successor(19), successor(9), successor(29).

             22
            /  \
          10    27
         /  \   / \
        2   17 25 29
           /  \
         15   19
         / \    \
       12  16   20
         \
         13

bstSuccessor(n)           // node n
  if (n->right != 0)
    return bstMin(n->right)    // find min of the right subtree
  else
    y = n->parent
    x = n
    while (y != 0 &&
        x == y->right)  // true if x is a right child of its parent
      x = y        // move x up
      y = y->parent    // move y up
    endwhile
    return y         // y is parent of x and x is left child of y

Delete

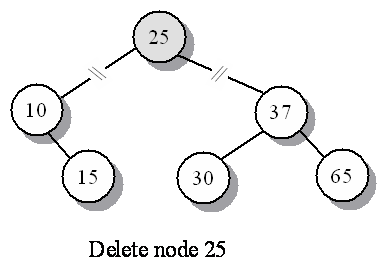
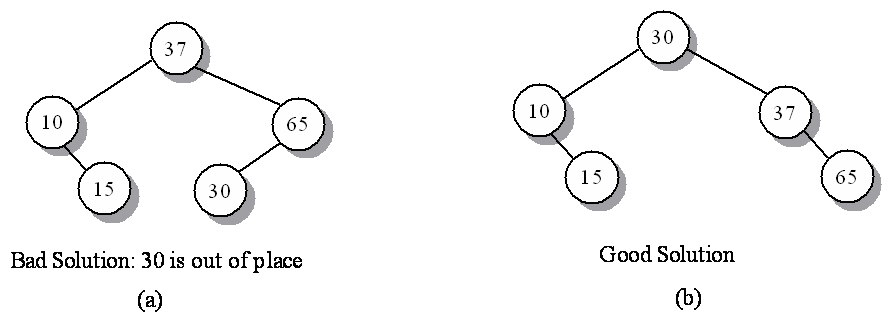
The binary search tree delete has the complication that a node may have children which are orphaned when the parent is deleted.

Binary search tree delete, 3 cases, d is the node to be deleted:

number of children	action
0	delete node `d`
1	splice out node `d`
2	More complicated, do the following: find node `s`, the successor of `d`. `s` is the minimum of `d`'s right subtree. Note that `s` has no left child. Replace node `d` with `s`, Two cases `s` is right child of `d` Effectively node `s` will move in to `d`'s spot by adjusting links. `d`'s left child becomes `s`'s left child (`s` had no left child) `d`'s parent becomes `s`'s parent `s` is not right child of `d` Effectively node `d`'s successor will move in to `d`'s spot by adjusting links. `s`'s parent's left child gets `s`'s right child (subtree). `d`'s left child becomes `s`'s left child (`s` had no left child) `d`'s right child becomes `s`'s right child (`s`'s old right child given up previously) `d`'s parent becomes `s`'s parent

Copy

node* copyTree (n)     // n points to root of subtree to copy
  if (n == 0)
    return 0
  else
    new_left = copyTree(n->left)
    new_right = copyTree(n->right)
    new_node = node(new_left, new_right, n->data)
    return new_node

What traversal is used?

Delete Tree

deleteTree(n)
  if (n != 0)
    deleteTree(n->left)
    deleteTree(n->right)
    delete n

What traversal is used?

Analyses

In general, for a binary tree,

the worst case depth for any leaf is O(n)

In a balanced binary tree the depth of all leaves is the same or 1 plus the least.

Balanced binary tree analyses, worst case (for each, why?),

operation	complexity
search	O(log₂ n)
minimum	O(log₂ n)
successor	O(log₂ n)
insertion	O(log₂ n)
deletion	O(log₂ n)

A red-black tree is a binary tree where nodes are assigned colors and certain properties are maintained, the maintainence of which insures that the tree will stay balanced.