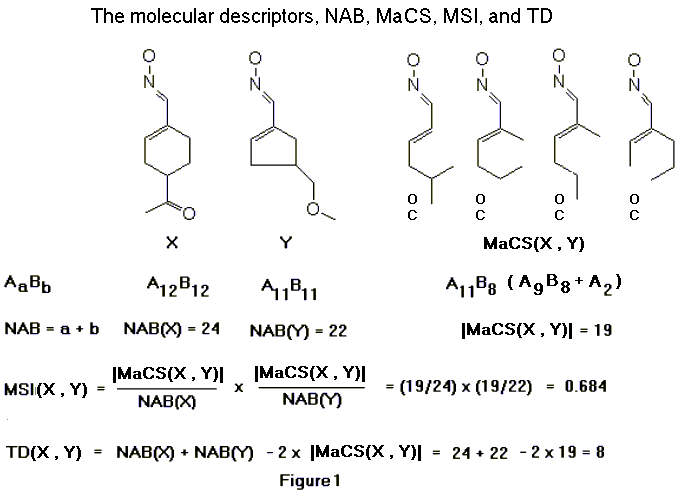
An Efficient Algorithm for Similarity Analysis of Molecules
* To whom correspondence should be addressed
Keywords: molecular similarity analysis, maximal common substructure, labeled graph isomorphism, subgraph isomorphism algorithm, maximal common labeled subgraph, maximal clique algorithm.
Abstract This paper describes a subgraph isomorphism algorithm for matching chemical graphs. It has been implemented in a computational chemistry program called TOPSIM (TOPological SIMilarity). Given a pair of molecules X and Y, TOPSIM finds a maximal common substructure (MaCS), a substructure with the greatest number of atoms and bonds (NAB) common to both molecules. A MaCS may consist of structural fragments and isolated atoms. This MaCS concept provides a basis for measures of pairwise molecular similarity and dissimilarity. The similarity of molecules X and Y is measured by the molecular similarity index, MSI(X,Y), and is defined as [|MaCS(X,Y)|/NAB(X)][|MaCS(X,Y)|/NAB(Y)], where |MaCS(X,Y)| is the number of atoms and bonds in the MaCS of X and Y, NAB(X) is the number of atoms and bonds in molecule X, and NAB(Y) is the number of atoms and bonds in molecule Y. The dissimilarity of molecules X and Y is measured by the topological distance, TD(X,Y), which is defined as NAB(X) + NAB(Y) – 2|MaCS(X,Y)|. To determine a MaCS of molecules X and Y, their structures are represented by labeled graphs X and Y respectively, in which vertices denote atoms, edges denote bonds, and the vertex and edge labels indicate atom and bond types. TOPSIM compares X and Y and identifies their maximal common subgraph (MCSG), based on identifying a maximal clique in a compatibility graph and adding in their common isolated atoms. The MCSG thus formed represents a MaCS of X and Y. TOPSIM then computes MSI(X,Y) and TD(X,Y) based on the NAB of the MaCS.
1 Introduction
A subgraph isomorphism algorithm for matching chemical graphs is described in this paper. It forms the basis of the computational chemistry program called TOPSIM (TOPological SIMilarity) [1,2]. Given a pair of molecules X and Y, TOPSIM computes the number of atoms and bonds (NAB) in their maximal common substructure (MaCS) with the greatest NAB value. To determine a MaCS of molecules X and Y, their structures are represented by labeled graphs X and Y respectively, in which vertices denote atoms, edges denote bonds, and the vertex and edge labels indicate atom and bond types. TOPSIM compares X and Y and identifies a maximal common subgraph (MCSG) of X and Y, a graph with the greatest number of vertices and edges that is a subgraph common to both X and Y. The MCSG is found by first identifying a MCES, a subgraph common to both X and Y which has the largest number of edges but no isolated vertices. A MCES can consist of multiple fragments. A fragment is a connected component in a graph. TOPSIM finds a MCES by constructing a compatibility graph C for X and Y. A maximal clique in C represents a MCES of X and Y. Next, the common isolated vertices (CIV) are found and the combination of a MCES and CIV forms a MCSG. The MCSG thus formed represents a MaCS of X and Y. A MaCS may consist of structural fragments and isolated atoms. This MaCS concept provides a basis for measures of pairwise molecular similarity and dissimilarity. The similarity of molecules X and Y is measured by the molecular similarity index, MSI(X,Y), and is defined as [|MaCS(X,Y)|/NAB(X)][|MaCS(X,Y)|/NAB(Y)], where |MaCS(X,Y)| is the number of atoms and bonds in the MaCS of X and Y, NAB(X) is the number of atoms and bonds in molecule X, and NAB(Y) is the number of atoms and bonds in molecule Y. The dissimilarity of molecules X and Y is measured by the topological distance, TD(X,Y), which is defined as NAB(X) + NAB(Y) – 2|MaCS(X,Y)|. An example to illustrate the molecular descriptors, NAB, MaCS, MSI, and TD, is given in Figure 1. In this example, there are four possible maximum common substructures for the molecules X and Y.
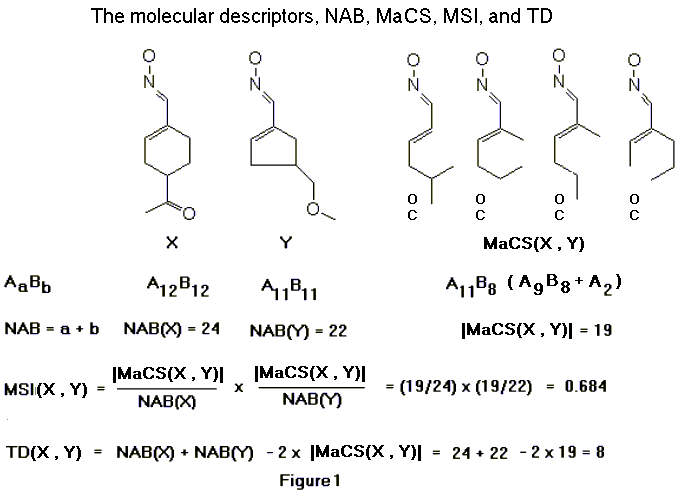
Molecular similarity analysis using molecular descriptors such as NAB, MaCS, MSI, and TD has been found to be very useful for searching molecular databases, selecting compounds for drug screening, predicting molecular properties, designing drugs, and modeling drug receptor sites [3-8]. This paper describes an algorithm that finds a MaCS of two molecules. The algorithm applies an extension of an earlier maximal clique algorithm [9] to identify a maximal common labeled subgraph of two labeled graphs. This algorithm is useful in the similarity analysis of molecules. The theoretical concept behind the algorithm is described, followed by a discussion of the basic algorithm and its improvements.
2 Theoretical Basis for TOPSIM's Subgraph Isomorphism Algorithm.
We use labeled graphs to represent molecular structures. A labeled graph can be defined mathematically as G = (V, E, t) where V is the set of vertices, E is the set of edges, and t is a function which maps the union of V and E to natural numbers. Moreover, G provides a chemical graph of a molecular structure if V represents the set of atoms, E represents the set of bonds, and t is a function which maps atoms and bonds to their types. For example, if x is an element from the set of bonds, then t(x) represents the bond order of x (e.g., a single bond) and if x is an atom then t(x) indicates the atom type for x (e.g., C, N, O). The labeled graph representation of the two molecules, displayed in Figure 2, is shown in Figure 3.
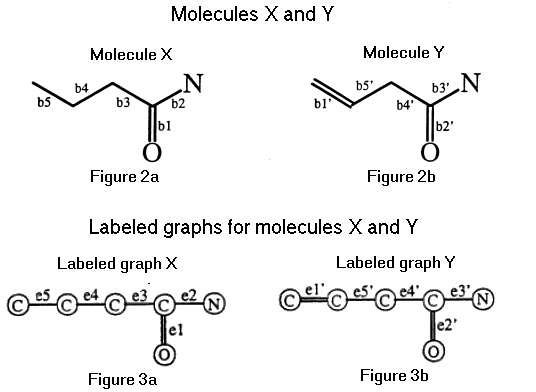
Two graphs G and K are said to be isomorphic if there is a one-to-one correspondence (mapping) between their vertex sets which preserves the adjacency of vertices. The mapping itself is called an isomorphism. Graphs G and K are edge isomorphic if there exists a one-to-one mapping between their edge sets that preserves adjacency of edges. The mapping is called an edge isomorphism. Since an edge is defined by its vertices, an isomorphism induces an edge isomorphism. However, the existence of an edge isomorphism h from graph G to K does not imply that there exists an isomorphism from G to K which induces h. Whitney [10] has shown that an edge isomorphism h from G to K is induced by an isomorphism from G to K if and only if h does not contain a triode-triangle interchange. An edge isomorphism h from G to K, contains a triode-triangle interchange if there exists a set of three edges {x, y, z} in G which forms a triode (triangle) such that the set of edges {h(x), h(y), h(z)} forms a triangle (triode) in K. An example of triode-triangle interchange is shown in Figure 4. Note that G is edge isomorphic with K, but G is not isomorphic with K.
The definitions of isomorphism and edge isomorphism may easily be extended to include labeled graphs. Labeled graphs G and K are isomorphic if there is an isomorphism between them that preserves types. Labeled graphs G and K are edge isomorphic if there is an edge isomorphism between them that preserves types. In the second case, preservation of types is defined as follows: Given graphs G = (Vg,Eg,tg) and K = (Vk,Ek,tk) and an edge isomorphism h:EgàEk, then types are preserved by h if and only if for edges x and y in Eg, three conditions are satisfied :
i. The types of the corresponding edges are equivalent (e.g., tk(h(x)) = tg(x)).
ii. The vertices of x have the same types as those of h(x).
iii. If x and y are incident at vertex i then h(x) and h(y) are incident at a vertex with the
same type as i. The converse must also be true.
Suppose G and K are labeled graphs with an edge isomorphism h between G and K that preserves types and does not contain a triode-triangle interchange. By the preceding paragraph, h is induced by an isomorphism that preserves types. Additionally, suppose that the labeled graphs G and K are subgraphs of labeled graphs G' and K', respectively. Then any labeled graph isomorphic to both G and K is a common subgraph of G' and K'. A common edge subgraph CES is a common subgraph that contains no isolated vertices (see Figures 5a-5c). Also, the chemical structure represented by CES is a substructure common to the chemical structures represented by G' and K'. A maximal common edge subgraph (MCES) of G' and K' is a common edge subgraph of G' and K' which has the largest number of edges (see Figure 5c).
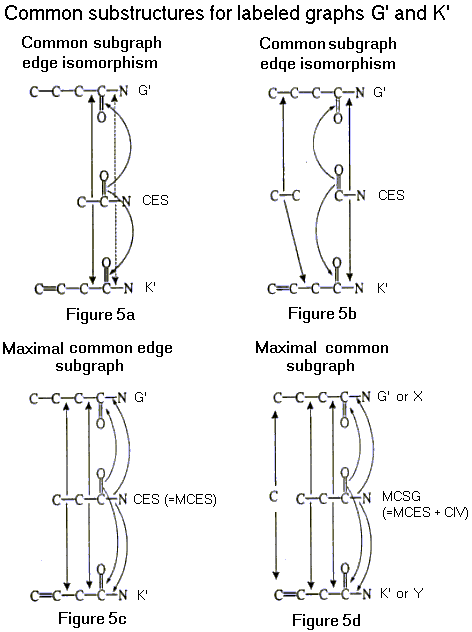
Let CSG be a common subgraph of G' and K'. Then CSG is isomorphic to a subgraph of both G' and K'. Additionally, there is an edge isomorphism without triode-triangle interchange between CSG and a subgraph of G' and an edge isomorphism without triode-triangle interchange between CSG and a subgraph of K'. The cardinality of a labeled graph (V,E,t) is defined by |V| + |E|, which is the sum of the number of vertices and edges. A CSG with maximal cardinality is a maximal common subgraph (MCSG) of G' and K' (see Figure 5d). The MCSG can be obtained by adding the common isolated vertices (see Figure 5d). The common isolated vertices (CIV) is defined as the common vertices in G' and K' that are not in MCES. Mathematically, CIV is given by CIV(G',K') = V(G') Ç V(K') – V(MCES(G',K')), where V(G') and V(K') denote the vertices of the graphs G'and K', respectively. This MCSG, which includes MCES and CIV, represents a MaCS of the molecules X and Y and is shown in Figure 5d.
A compatibility graph is used to compute the MCES. Given two labeled graphs G = (Vg,Eg,tg) and K = (Vk,Ek,tk), then the compatibility graph C(G,K) = (Vc,Ec) is defined by the following definitions of Vc and Ec. First, let
Vc = {(x,y) | x Î Eg, y Î Ek, tg(x) = tk(y) and the vertices which define x are same type as those which define y}.
Two vertices, Vc(i) = (x,y) and Vc(j) = (a,b) are compatible if and only if edges x and a are incident at the same type of vertex in G as y and b are in K, respectively. If a pair of edges (x,y) are not incident, we say they are incident at a vertex of type 0. Then Ec is defined as
Ec = {( Vc(i),Vc(j) ) | 1 £ i,j £ |Vc| and Vc(i) is compatible with Vc(j)}.
In other words, an edge is drawn between two vertices in C(G,K) if and only if the edge pairs they represent can both exist in a subgraph edge isomorphism between G and K which preserves types. A clique in C(G,K) defines a subgraph edge-isomorphism between G and K. A maximal clique, such that its corresponding edge-isomorphism contains no triode-triangle interchanges, represents the MCES. It is instructive to illustrate how a compatibility graph is generated. The concept of extended edge is useful here. An extended edge in a labeled graph consists of an edge together with its two vertices and its edge and vertex labels. Figure 6 represents the extended edge matching for the molecular graphs shown in Figure 3.a-b.
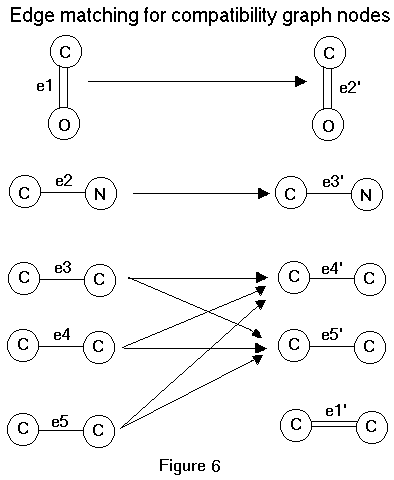
In order to form the compatibility graph, we first represent the molecules X and Y as labeled graphs X and Y (Figure 7a). Then the labeled graphs X and Y are represented by relational line graphs L(X) and L(Y), respectively (Figure 7b). Each edge in a relational line graph represents a relationship between the pair of vertices that define it. In this case, an edge between two vertices means that the extended edges represented are incident on each other. The edge label indicates the type of vertex (atom) they are incident upon. In Figure 7b, the nodes i (or e1:C=O) and ii (or e2:C-N) of graph L(X) are joined by an edge labeled with an Ic which means that the relation incident at a carbon vertex holds between the two nodes. A compatibility graph (Figure 7c) is then drawn using these two relational line graphs L(X) and L(Y) (see Figure 7b).
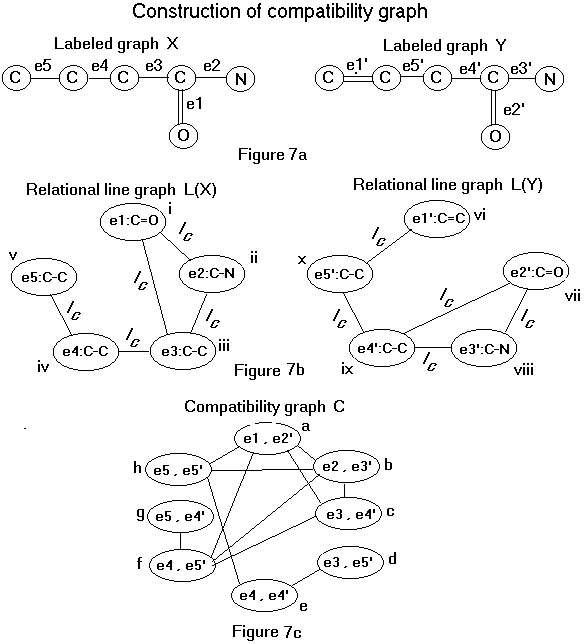
Note that the nodes in the compatibility graph (Figure 7c) can be partitioned into groups based on the first member of the ordered pair of extended edges comprising each node. For this example, there are five groups, namely {a}, {b}, {c,d}, {e,f}, and {g,h}. A subgraph of a graph is a clique if every pair of vertices are connected. The method for finding a clique in the compatibility graph can be visualized as a depth first search (DFS) traversal of a tree. Each level in a tree corresponds to a group. A group is composed of nodes such that for any two nodes in a group (ei,ej), (ek,el) the following condition always hold: ei=ek and ej¹el where ei,ekÎEg and ej,elÎEk. In the example shown in Figure 8, the groups and levels in the tree are represented in the same order i.e., group {a} is represented at level 1 and so on. The selection of a node depends on it being compatible with nodes already selected. We keep track of selected nodes. In order to find a maximal clique, it is necessary to do both forward traversals and backtracking. A forward traversal may result in addition of a node and a backtracking step may result in deletion of a node (Figure 8).
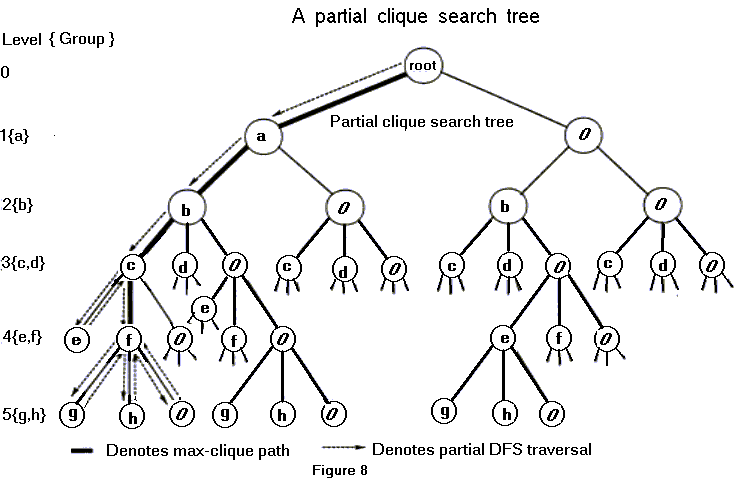
Although the clique search algorithm used in TOPSIM can be visualized as a depth first search (DFS) traversal of a tree, its implementation does not require a tree data structure explicitly, nor does the entire search space need to be represented in memory at once.
3 Algorithm Used to Identify a Maximal Clique.
An explanation of how the Max-Clique Search Algorithm works is given next. The algorithm generates a list of nodes that represents a clique path in the search tree by systematically selecting one node at a time from successive levels, until it is not possible to lengthen it further. When a node is being considered, the forward search part of the algorithm first checks to see if this node is a legal node, and if it is the algorithm next checks to see if the size of the new clique formed is as large or larger than the current largest clique, in which case it is saved. A node is legal if it is connected to every other node in the clique and does not induce triode-triangle interchange. At a given level n of the tree, at most one node can be selected. Note the initial value of n is 0 which represents the root of the tree. Following the selection of a node at level n, the algorithm seeks to expand the clique by adding the next available legal node at level n+1. After considering all the nodes in a group at level n+1, a null node is registered for level n+1 and an attempt is made to select a node from level n+2 without including a node from level n+1. A null node is a right-most child for each node and always stores the value 0. When all possible nodes have been considered that allows movement in a forward direction away from the root of the tree, then the algorithm backtracks and tries to expand along a different branch of the tree. When backtracking occurs, the nodes are removed from the list one at a time until a node is reached from which the remaining clique can be re-expanded or until all possibilities are exhausted. The length of the longest list (excluding any null node entries) as well as its composition is maintained. This information is updated, as needed. Further details are given in [1-2].
To speed up the process of identifying a maximal clique, we establish a theoretical upper bound on the size of a maximal clique and also determine a practical lower bound by rapidly identifying a relatively large clique in the compatibility graph. These bounds are used to limit the search of the Basic Max-Clique Search Algorithm. While the theoretical upper bound places a limit on the size of a maximal clique formable, it does not ensure that one of that size exists. To determine the practical lower bound, a maximal clique is identified in the pruned compatibility graph with a reduced set of nodes. The clique found in the pruned compatibility graph is used as a starting point for finding a maximal clique in the complete compatibility graph. A node (ei,ej) in the compatibility graph generated from a pair of molecules is pruned if either of the following two cases occur. In the first case, both molecules contain aromatic rings and only one of the set of extended edges incident upon ei or ej contains aromatic bonds. In the second case, one or none of the molecules contains an aromatic ring and the set of extended edges incident upon ei or ej is not a subset of the set of extended edges incident on ej or ei, respectively. As an example for the second case, for the node f {i.e., (e4,e5')} in Figure 7c, the set S1 of extended edges incident upon e4 is {(e5:C-C),(e3:C-C)} and the set S2 of extended edges incident upon e5' is {(e1':C=C),(e4':C-C)}. Since neither S1 or S2 is a subset of the other, node f is pruned. By pruning graph nodes based on the above two cases, we can normally obtain a maximal clique based on this reduced set of nodes rapidly, yielding a practical lower limit on a maximal clique attainable in the complete compatibility graph. With this approach, the running time of this algorithm is very rapid for two dissimilar molecules. Overall, this improves the average-case running time of the algorithm.
Significant improvements in running time can be obtained by first sorting each group in descending order based on node connectivity and next by sorting the groups in descending order based on the connectivity of the first node in each group [1]. The connectivity of a graph node n refers to the number of mutually independent nodes that are adjacent to node n in the compatibility graph. Any two graph nodes (ei,ej) and (ek,el) in the compatibility graph are independent if and only if ei¹ek and ej¹el. The connectivity will never exceed the actual number of incident edges. This involves extra processing prior to executing the Max-Clique Search Algorithm on the entire graph, but reduces the number of checks required. This helps in detecting a maximal clique at a very early stage. The Max-Clique Search Algorithm uses an edge isomorphism rather than an isomorphism for labeled graphs, which in some cases can reduce the number of possibilities considered by a factor of one million [11].
4 Algorithm Improvements
Additional techniques which significantly decrease the average running time of the TOPSIM kernel have been implemented. One method involves the order in which molecular data is presented to the function which generates the compatibility graph. The smaller of the two molecules (the one with the lower NAB value) is selected as the base compound since the maximum NAB value of a common substructure can never be greater than this. So the correct order of the two molecules is obtained by taking the smaller molecule as the first input and the larger one as the second input. For molecules having the same NAB size, the order is not important. This technique is particularly effective, yielding reductions in running time ranging from 50% to 99.97% when comparing the same molecules in incorrect order as compared to correct order. The user can enter the compounds in either order in the TOPSIM program, since the final order of the molecules is determined by the program before it generates the compatibility graph. Additionally, the nodes within a group are sorted so that they are in non-increasing order based on connectivity. A significant improvement in the running time is made possible by combining "group reordering", together with the above mentioned intra-group node sorting. The groups are sorted in descending order based on node connectivity of the first node in each group. This involves extra processing prior to the running of the Max-Clique Search Algorithm but leads to an overall improvement [1]. Certain extra information is maintained at each node about its neighbors so that the TOPSIM can find a maximal clique faster. TOPSIM is also efficient in terms of memory utilization, as it uses dynamic memory allocation, which reduces the memory storage required per molecule. This gave a 50% reduction of memory required, compared to the fixed allocation method, for sample molecular databases tested [1]. Dynamic allocation also eliminates the limitation placed on the molecular size by fixed allocation. An object-oriented approach to data organization is used which improves program organization, readability and expandability while maintaining efficient data access.
5 Summary
In this paper, a labeled subgraph isomorphism algorithm is presented which allows the similarity between two molecules to be evaluated. A labeled graph is used to represent a molecule with vertices representing atoms, edges representing bonds, vertex labels specifying the atom type, and edge labels specifying the bond type. The algorithm converts the labeled graph representations of two molecules into a compatibility graph. Then a modified maximal clique algorithm is used to find the maximal clique which represents the largest common substructure (excluding common isolated atoms) for the two molecules. A maximal common substructure is obtained by combining a largest common substructure and the common isolated atoms. The size of a maximal common substructure is then used to define both a molecular similarity index and a topological distance for two molecules. These molecular descriptors have been found to be very useful for a number of applications, including searching molecular databases, selecting compounds for drug screening, drug designing, predicting molecular properties, and modeling drug receptor sites.
References
1. Durand, P. J. An Improved Program for Topological Similarity Analysis of Molecules, MS Thesis, Kent State University, Kent, Ohio, 1996.
2. Pasari, R. Visualization and Reduction Algorithms for Similarity Analysis of Molecules, MS Thesis, Kent State University, Kent, Ohio, 1999.
3. Johnson, M.; Naim, M.; Nicholson, V.; Tsai, C. C. Unique Mathematical Features of the Substructure Metric Approach to Quantitative Molecular Similarity Analysis, Studies in Physical and Theoretical Chemistry, 51 (1987), 219-225
4. Tsai, C.C.; Johnson, M.; Nicholson, V.; Naim, M. A. Topological Approach To Molecular Similarity Analysis and Its Application, Studies in Physical and Theoretical Chemistry, 51 (1987), 231-236.
5. Wild, D. J.; Willett, P. Similarity Searching in Files of Three-Dimensional Chemical Structures. Implementation of Atom Mapping on the Distributed Array Processor DAP-610, the MasPar MP-1104, and the Connection Machine CM-200, J.Chem. Inf. Comput. Sci. ,34(1994), 224-231.
6. Johnson, M. A.; Maggiora, G. M. Concepts and Applications of Molecular Similarity, Wiley-Interscience Publication, 1990.
7. Lesniewski, M. L.; Parakulam, R. R.; Taylor-McCabe, K. J.; Marquis II, M. A.; Tsai, C. C. QSAR Studies of Antiviral Agents Using Structure-Activity Maps, Internet Journal of Chemistry 2, 7 (1999). http://www.ijc.com/articles/1999v2/7/
8. Parakulam, R. R.; Lesniewski, M. L.; Taylor-McCabe, K. J.; Tsai, C. C. QSAR Studies of Antiviral Agents Using Molecular Similarity Analysis and Structure-Activity Maps, SAR and QSAR in Environmental Research 10 (1999), 1-32.
9. Bron, C.; Kerbosch, J. Algorithm 457: Finding All Cliques in an Undirected Graph, Communications of the Association for Computing Machinery 16 (1973), 575-577.
10. Witney, H. Congruent Graphs and the Connectivity of Graphs, Amer. J. Math., 54 (1932), 150-168.
11. Nicholson, V.; Tsai, C. C.; Johnson, M.; Naim, M. A Subgraph Isomorphism Theorem For Molecular Graphs, Studies in Physical and Theoretical Chemistry, 51 (1987), 226-230.