Straight Lines and Their Equations

The straight line is one of the most basic concepts in geometry, next only to the concept of a point. Here are some facts about straight lines.

• A straight line is straight because any two segments on the line form an 180-degree angle with each other.
• The shortest path between any two points on a straight line is through the points connecting them on the line.
• The slope of a straight line measures how slanted the line is.
• The y-intercept is the y coordinate of the point where the line intercepts the y-axis and the x-intercept is the x coordinate of the point where the line intercepts the x-axis.

  The y-intercept of the line in this graph is exactly   .

  The x-intercept of the line in this graph is almost   .

• A straight line in the xy-plane always has an equation in this general form

  a x + b y + c = 0

  where a is the coefficient of x, b is the coefficient of y, and c is the constant term.

  A straight line always has an equation in this form and the graph of any equation in this form is a straight line.

  Any point with coordinates (x1, y1) is on the line if it satisfies the equation which means if you subsitute the value x1 for x and the value y1 for y in the euqation, the result a x1 + b y1 + c is actually equal to zero.

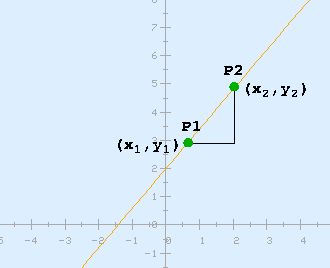Assuming the x-axis represents the horizontal and the y-axis reprents the vertical, then the slope of a straight line measures how slanted or steep the line is relative to the horizontal or vertical. Specifically, the slope is the change in y per unit change in x. For example, a horizontal line has slope zero and a vertical line has slope infinity. In general, the slope is:

Written out explicitly, this means

computed using any two points P1 and P2 on the line.

Given the equation of a line, we can find its slope using the above definition. But there is another way that may be easier. By putting the equation of a line in the slope-intercept form

y = m x + b

you can easily obtain the value for b, the y-intercept, and the value for m, the slope.

1. Let's try taking an equation and transform it into the slope-intercept form. First, enter a line equation of your choosing:

    x +   y +   = 0  Start

   And it is displayed here. Numbers are rounded to the nearest hundredth.

   You can transform this equation into the slope-intercept form by solving for y in terms of x through a sequence of steps, by adding, subtracting, multiplying or dividing both sides with the same quantity.

2. Enter a number or a multiple of x (for example 2 x and -4 x) and click a button and the operation will be applied to both sides of the latest equation and produce an equvalent new equation:

                      

    x          

            

3. Try and do another equation.

Here is a diagram where you can interactively enter a straight line. Then you can move the y-intercept or rotate the line by dragging the intercept point or the line. As the line changes, you'll also see the equation for the line change.