[3.1]- The Role of the Lexical Analyzer

The lexical analyzer or scanner is the first phase of a compiler: its main task is to read the input characters and produce a sequence of tokens for the syntax analyzer. It is usually implemented as a subroutine which the syntax analyzer calls whenever it wants the next token: the lexical analyzer returns a token and then waits for the next call.

A secondary task of the lexical analyzer is to ignore white space (spaces, tabs, and newline characters in the source) and comments. Another task might be to keep track of line numbers so meaningful error messages can be generated.

Tokens, Patterns, Lexemes

The terms token, pattern, and lexeme have specific meanings. The lexical analyzer returns a token of a certain type to the parser whenever it sees a sequence of input characters, a lexeme, that matches the pattern for that type of token.

This table shows the patterns of the tokens for the source language of the coding projects. For example, the pattern for the RELOP token contains six lexemes (=, <>, <, <=, >=, and >) so the lexical analyzer should return a RELOP token to the parser whenever it sees any one of the six. Many tokens such as IFTOK, THENTOK, etc., have single-lexeme patterns.

In this table the patterns for the ID and NUM tokens are described by regular expressions which are discussed later in section 3.3. Informally, a lexeme for the ID token must start with a letter followed by zero or more letters and digits.

Lexical analysis is complicated in some languages. FORTRAN, for example, allows white space inside of lexemes. The FORTRAN statement:

     DO 5 I = 1.25

but the FORTRAN statement:

     DO 5 I = 1,25

Before the lexical analyzer can produce the first token it must look ahead to see if there is a dot or a comma in this statement.

Most languages have keywords, strings of letters that have pre-defined meanings so they can not be used as identifiers. For example, keywords in Pascal are: if, then, else, etc. The PL/I language does not reserve its keywords so distinguishing between a keyword and an identifier is very complicated. For example,

    IF THEN THEN THEN = ELSE; ELSE ELSE = THEN;

Attributes for Tokens

The pattern for the RELOP token in Pascal contains six lexemes: the syntax analyzer only needs to know that the token is a relational operator but later phases will have to know which of the six relational operators is specified so the lexical analyzer must return this attribute with the RELOP token.

The lexical analyzer must also return attributes with other multi-lexeme tokens: the UNARYOP, ADDOP, MULOP, BCONST, ID, and NUM tokens. A pointer to the symbol table entry is all that is required for an ID token. An easy way to handle a NUM token is to store its lexeme in the symbol table and return a pointer to that entry. One way to handle the other multi-lexeme tokens is to pre-store all their lexemes in the symbol table so the lexical analyzer can return a pointer to a symbol table entry in all cases.

Lexical Errors

A lexical error is a sequence of characters that does not match the pattern of any token. The most common causes of a lexical error are:

• the addition of an extraneous character;
• the removal of a character that should be present;
• the replacement of a correct character with an incorrect character; and
• the transposition of two characters.

The theoretically best way of handling a lexical error is to find the closest character sequence that does match a pattern but this will take too much time and is never used in a practical compiler. The easiest way to handle a lexical error is to store the bad character in the symbol table and return an ERROR token to the syntax analyzer with a pointer to the symbol table entry. To simplify the coding projects none of their test files will have any lexical errors.

[7.6] - Symbol Tables

The symbol table keeps track of information about the symbols (identifiers) that the source program is using: names of scalars, arrays, and functions, etc.

Often, numbers are also put in the symbol table because their values must be stored somewhere: putting numbers into the symbol table is easier than creating a separate table for them.

Usually, keywords like if, while, and real, are also put in the symbol table since their lexemes look like the lexemes of identifiers. The keywords are pre-loaded into the symbol table before any of the source program is read so the first time the source program uses a keyword it will be assigned the proper token-type.

The lexical analyzer can be simplified by also pre-loading the other lexemes like (, ], :=, and <=, into the symbol table.

The Data Structure of a Symbol Table: The compiler should be able to grow the symbol table dynamically: a table of fixed size would have to be very large to accommodate the worst-case source program and most of that storage would be wasted whenever a source program of a typical size is compiled.

Adding new entries and finding existing entries should both be efficient operations. It is easy to add new entries to a linear linked list but finding existing entries will be very slow for large programs with many symbols. A binary search tree like a Red-Black tree would be satisfactory but coding is complicated.

Hash Tables: Usually the symbol table is implemented with a hash function to steer each entry to one of a number of linear linked lists: a good hash function will sprinkle the entries across many lists so every list is short enough to be searched efficiently. Figure 7.34 in the text illustrates a hash table, an array of 211 list headers with indices ranging from 0 to 210. Each list header points to the start of a linked list of symbol table entries (a list header is NULL if its list is empty.) To find an entry for a given lexeme: the lexeme is sent to a hash function which returns an integer in the range of 0 to 210; that integer is used as an index to select one of the headers in the hash table; and that header is used to search the corresponding linked list sequentially for an entry with the given lexeme.

Hash Functions: Figure 7.36 in the text shows the performance of a number of hash functions. Four of the functions seem to have good performance: hashpjw , x65599 , quad , and x16 .

Figure 7.35 shows the C code for hashpjw .

x65599 initializes h to 0, performs h = (65599 * h + (ASCII-value of character)) mod 211 for each character in the lexeme, and then returns h .

x16 is similar to x65599 except that the constant multiplier is 16 instead of 65599.

quad splits the lexeme into 4-character groups, adds the groups together as though they were integers, and returns their sum modulo 211.

Regardless of the hash function, hashing seems to work much better when the size of the hash table is a prime number like 211.

Storing the Lexemes: Most source languages do not impose any limit on the length of a symbol name. Most programmers use only short symbol names (e.g., 10 characters or less) but the compiler must also be capable of handling a very long symbol name with 100 characters or more.

Figure 7.32(b) in the text shows one method of storing the lexemes. Lexemes are stored serially as they are first encountered in a large array of a few thousand characters with each lexeme followed by an end-of-string character. The lexeme field of each symbol table entry is only a short 2-byte integer to hold the starting location of the lexeme in the large array. This method works as long as the sum of all lexeme lengths (including their end-of-string characters) does not exceed the length of the large array.

Alternatively, if the compiler is written in C or C++, each lexeme can be stored in a dynamic storage item that is just large enough to hold it and its end-of-string character. Each symbol table entry is stored in another dynamic storage item of fixed size containing a pointer to the lexeme item.

The Scope of Symbols: The scope of symbols is best illustrated with an example like the Pascal source program below:

    program main(input, output);
    var x, y : integer;
    var z   : real;
    function foo(a : real) : real;
        var x : real;
        begin               { body of foo function }
            x := 2.0 * a;
            y := y + 1;
            foo := x + 5.0
        end;
    begin                   { body of main program } 
        y := 0 ;
        x := 0 ;
        z := foo(6.0)
    end. 

This example has three global variables: two integers, x and y , and one real, z . Function foo has two internal real variables, a and x , and a real return value, foo . A global integer and a real variable local to foo share the same name, x : the scope rules for Pascal tell us that x in the body of foo denotes the local real variable while x in the body of the main program denotes the global integer. Both the global integer and the local real must have an entry in the symbol table and the two entries will have the same lexeme: the symbol table search operation must be designed to always return a pointer to the correct entry.

When compiling the body of a function the search operation should return the local variable instead of the global variable whenever there are duplicated lexemes. When searching a linked list the FIND function will return the entry closest to the start of the list and globals are inserted before local variables so the INSERT function should always insert each entry at the start of the list.

When the body of a function has been completely compiled all variables local to that function should be flagged as unsearchable. One way to do this is to use an integer Scope field in each entry to keep track of its scope: the scope field will be 0 for a global, positive for a local variable, and negative for an entry that is unsearchable. The syntax analyzer maintains the current scope of the compilation in a global integer, CurrentScope , that the INSERT function copies into the Scope field of each entry it inserts. The syntax analyzer also negates the Scope field of the local entries whenever a function has been completely compiled. The FIND function should ignore any entry with a negative Scope field.

[3.3] - Specification of Tokens

An alphabet is a finite set of symbols. Typical examples of symbols are letters and characters. The set {0, 1} is the binary alphabet . ASCII and EBCDIC are two examples of computer alphabets.

Strings

A string over some alphabet is a sequence of symbols drawn from that alphabet. For example, banana is a sequence of six symbols drawn from the ASCII alphabet. The empty string, denoted by epsilon, , is a special string with zero symbols.

If x and y are two strings then the concatenation of x and y, written xy, is the string formed by appending y after x . For example if x = dog and y = house then xy = doghouse.

String exponentiation concatenates a string with itself a given number of times: x² = xx ; x³ = xxx ; x⁴ = xxxx ; etc. By definition x⁰ is the empty string, , and x¹ = x . For example, if x = ba and y = na then xy² = banana.

Languages

A language is a set of strings over some fixed alphabet: the set may contain a finite number or an infinite number of strings.

If L and M are two languages then their union, denoted by L |_| M, is the language containing every string in L and every string in M (any string that is in both L and M appears only once in L |_| M ).

If L and M are two languages then their concatenation, denoted by LM, is the language containing every string in L concatenated with every string in M .

For example if L = {dog, ba, na} and M = {house, ba} then L |_| M = {dog, ba, na, house} and LM = {doghouse, dogba, bahouse, baba, nahouse, naba}.

Language exponentiation concatenates a language with itself a given number of times: L² = LL, L³ = LLL, L⁴ = LLLL, etc. By definition L⁰ = {} and L¹ = L .

The Kleene closure of a language L, denoted by L *, equals L⁰ |_| L¹ |_| L² |_| L³ |_| L⁴ |_| ...

For example, if L = {a, b} then L * = {, a, b, aa, ab, ba, bb, aaa, aba, baa, bba, aab, abb, bab, bbb, ... }.

The positive closure of a language L, denoted by L⁺, equals L¹ |_| L² |_| L³ |_| L⁴ |_| ...

For example, if L = {a, b} then L⁺ = {a, b, aa, ab, ba, bb, aaa, aba, baa, bba, aab, abb, bab, bbb, ... }.

Let L = {A, B, ... , Z, a, b, ..., z} be the set of all capital and lower-case letters and let D = {0, 1, ... , 9} be the set of all digits. Then:

• L |_| D is the set of all letters and digits.
• LD is the set of strings consisting of a letter followed by a digit.
• L⁴ is the set of all four-letter strings.
• L * is the set of all strings of letters including the empty string, .
• L (L |_| D )* is the set of all strings of letters and digits that begin with a letter.
• D⁺ is the set of all strings of one or more digits.

Regular Expressions

Every regular expression specifies a language according to the following rules:

1. is a regular expression that denotes {}, the set containing just the empty string.

2. If a is a symbol in the alphabet then the regular expression a denotes {a}, the set containing just that symbol.

3. Suppose s and t are regular expressions denoting languages L(s ) and L(t ), respectively. Then:
   • (s ) | (t ) is a regular expression denoting L(s ) |_| L(t ).
   • (s )(t ) is a regular expression denoting L(s )L(t ).
   • (s )* is a regular expression denoting L(s )*.
   • (s ) is another regular expression denoting L(s ) so we can put extra pairs of parentheses around regular expressions if we desire.

Unnecessary parentheses can be avoided in regular expressions using the convention that Kleene closure, *, is left-associative and takes precedence over concatenation which is left-associative and takes precedence over union, |, which is also left-associative.

Regular Definitions

A regular definition gives names to certain regular expressions and uses those names in other regular expressions. As an example:

letter	-->	A | B | ... | Z | a | b | ... | z
digit	-->	0 | 1 | ... | 9
id	-->	letter ( letter | digit )*

defines letter to be the regular expression for the set of all upper-case and lower case letters in the English alphabet, digit to be the regular expression for the set of all decimal digits, and id to be the regular expression for all strings of letters and digits that begin with a letter. Note that id is the pattern for the Pascal identifier token.

The pattern for the Pascal number token can be specified as follows:

digit	-->	0 | 1 | ... | 9
digits	-->	digit digit*
optional_fraction	-->	. digits |
optional_exponent	-->	( E ( + | - | ) digits ) |
num	-->	digits optional_fraction optional_exponent

This definition says that an optional_fraction is either a decimal point followed by one or more digits or it is missing (the empty string). An optional_exponent is either the empty string or it is the letter E followed by an optional + or - sign, followed by one or more digits.

Notational Shorthands

If r is a regular expression then:

(r )⁺ = r r *

and r ? = (r | ).

With these shorthand notations one can write:

num	= digits (. digits)? (E ( + | - )? digits)?
	= digit+ (.digit+)? (E (+ | - )? digit+)?

[3.4] - Recognition of Tokens

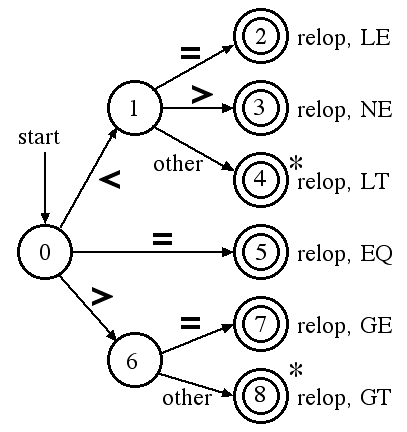
One way to recognize a token is with a finite state automaton following a particular transition diagram. For example, the transition diagram for the RELOP token of Pascal is:

The start state for this diagram is state 0. If the input character agrees with one of the arrows leaving that state then the analyzer goes to the state at the end of that arrow and examines the next input character. If none of the arrows leaving a state agrees with the input character then this particular transition diagram does not apply and the analyzer should return to the first input character and try the diagram for some other token. States with double circles are accept states where the analyzer can return a token to the caller. States with stars, *, indicate places where the last input character read must be returned to the input.

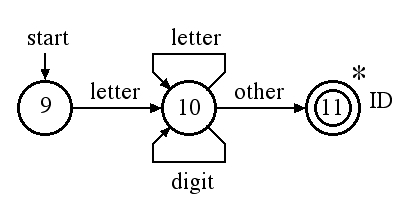
The transition diagram for the ID token of Pascal is:

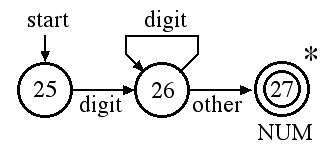
The recognition of the NUM token of Pascal can be done with three different transition diagrams. The first diagram accepts real numbers with exponents:

If the first diagram fails to reach its accept state then we should try the second diagram which accepts real numbers with fractions but no exponents: If the second diagram also fails then we should try the third diagram which accepts integers:

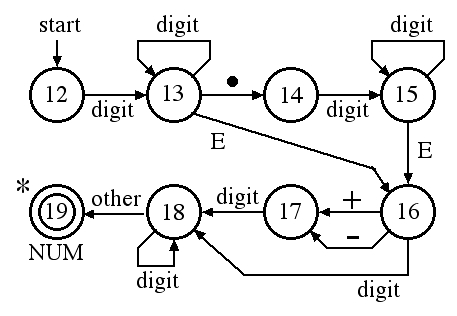
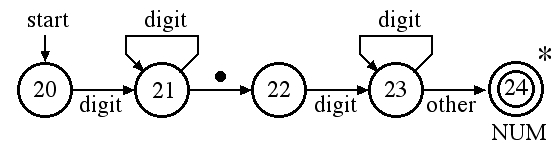
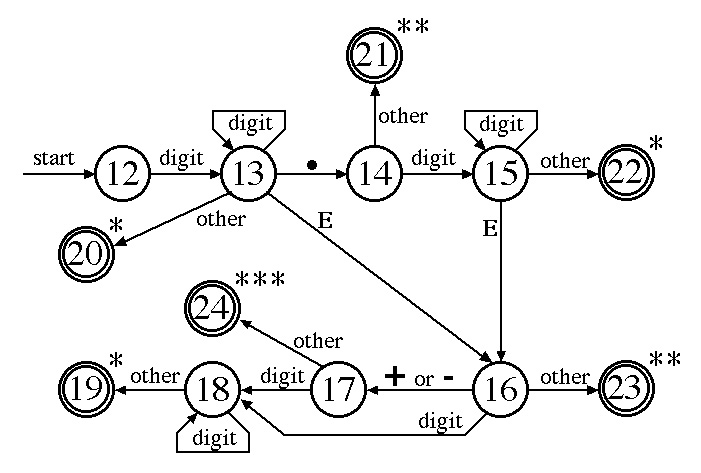
One can combine the three diagrams for unsigned numbers into one diagram but some of the accept states in this diagram have multiple stars to indicate that two or more characters must be pushed back onto the input:

As shown on this diagram, the number of characters that must be pushed back onto the input is: one if accept state 19, 20, or 22 is reached; two if accept state 21 or 23 is reached; and three if accept state 24 is reached. The number is real if state 15 or 18 (or both) is encountered by the transition - if neither state 15 nor state 18 is encountered then the number is an integer.

One can use transition diagrams to implement a lexical analyzer: the analyzer has a large case statement with a case for each state in the diagrams. Figure 3.15 shows the code for a fail() function that is called whenever the analyzer must try another diagram.

Click here for the Project 1 assignment.
Click here for a number of hints you can use in coding Project 1.

[3.5] - A Language for Specifying Lexical Analyzers

lex is one of a number of tools one can use to create a lexical analyzer from a description based on regular expressions. Figure 3.17 illustrates the steps:

1. lex creates a C code file, lex.yy.c, from a description of the analyzer written in the Lex language;
2. lex.yy.c is fed into a C compiler to produce the object program of the lexical analyzer, a.out ;
3. a.out will analyze an input source file lexically to produce a sequence of tokens.

Figure 3.18 shows the Lex description for an analyzer that recognizes white-space, identifiers, numbers, and relational operators.

lex is available on the UNIX machines of the department but you should not use it for Project 1: it is better to get the experience of writing your own lexical analyzer and it is doubtful that using lex is any simpler. We mention lex in this course only because you might want to use it in the future if you ever get involved in a compiler project.

[3.6] - Finite Automata

A recognizer for a language is a program that takes an input string x and answers yes if x is in the language or no if x is not in the language. One can compile any regular expression into a recognizer by constructing a generalized transition diagram called a finite automaton.

Nondeterministic Finite Automata: A Nondeterministic Finite Automaton or NFA for short consists of:

1. a set of states S ;
2. a set of input symbols called the input symbol alphabet;
3. a transition function move that maps state-symbol pairs to sets of states;
4. a state s₀ called the initial state or the start state;
5. a set of states F called the accepting or final states.

An NFA accepts an input string x if and only if there is some path in the transition graph from the start state to some final state such that the edge labels along this path spell out x. The following table shows the paths for three of the strings that the NFA of Figure 3.19 accepts:

   a      b      b
0 ---> 1 ---> 2 ---> 3

   a      a      b      b
0 ---> 0 ---> 1 ---> 2 ---> 3

   b      a      b      b
0 ---> 0 ---> 1 ---> 2 ---> 3

Note that there may be several paths that a given input string might take through an NFA - if at least one such path ends in a final state then the string is accepted. The language defined by an NFA is the set of input strings it accepts. Figure 3.21 shows an NFA that uses -transitions to define the language: a a* | b b* - the transition table for this NFA is:

State	Input Symbol
	a	b
0	-	-	{1,3}
1	{2}	-	-
2	{2}	-	-
3	-	{4}	-
4	-	{4}	-

Deterministic Finite Automata: A deterministic finite automaton or DFA for short is a special case where:

1. there are no -transitions; and
2. for each state s and input symbol a there is at most one edge labeled a leaving s.

Conversion of an NFA into a DFA: It is hard for a computer program to simulate an NFA because the transition function is multi-valued. Fortunately, the Subset Construction Algorithm will convert an NFA for any language into a DFA that recognizes the same language (it is closely related to an algorithm in Chapter 4 for constructing LR parsers.)

Each entry in the transition table of an NFA is a set of states; each entry in the table of a DFA is just a single state - the basic idea behind the NFA-to-DFA construction is that each DFA state corresponds to a set of NFA states. For example, let T be the set of all states that an NFA could reach after reading input: a₁, a₂, . . . , a_n - then the state that the DFA reaches after reading a₁, a₂, . . . , a_n corresponds to set T. Theoretically, if the number of states in the NFA is n then the DFA might have 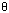( 2ⁿ ) states but this worst case is a very rare occurrence.

Subset construction (algorithm 3.2) uses certain operations to keep track of sets of NFA states - if s is an NFA state, T is a set of NFA states, and a is a symbol in the input alphabet then:

Operation	Description
-closure(s)	Set of NFA states reachable by -transitions from state s.
-closure(T)	Set of NFA states reachable by -transitions from every state s in T.
move(T,a)	Set of NFA states to which there is a transition on input symbol a from some state s in T.

Figure 3.26 shows an algorithm for computing the -closure function. The subset construction algorithm shown in Figure 3.25 constructs a set of states, Dstates, and a transition table, Dtran, for the DFA.

The first iteration of the while-loop:

• marks A;
• computes -closure(move(A, a)) = -closure(move({0, 1, 2, 4, 7}, a)) =
  -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8};
• enters B = {1, 2, 3, 4, 6, 7, 8} as an unmarked state in Dstates;
• sets Dtran[A, a] = B;
• computes -closure(move(A, b)) = -closure(move({0, 1, 2, 4, 7}, b)) =
  -closure({5}) = {1, 2, 4, 5, 6, 7};
• enters C = {1, 2, 4, 5, 6, 7} as an unmarked state in Dstates; and
• sets Dtran[A, b] = C.

The second iteration of the while-loop:

• marks B;
• computes -closure(move(B, a)) = -closure(move({1, 2, 3, 4, 6, 7, 8}, a)) =
  -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = B ;
• sets Dtran[B, a] = B;
• computes -closure(move(B, b)) = -closure(move({1, 2, 3, 4, 6, 7, 8}, b)) =
  -closure({5, 9}) = {1, 2, 4, 5, 6, 7, 9};
• enters D = {1, 2, 4, 5, 6, 7, 9} as an unmarked state in Dstates; and
• sets Dtran[B, b] = D.

The third iteration of the while-loop:

• marks C;
• computes -closure(move(C, a)) = -closure(move({1, 2, 4, 5, 6, 7}, a)) =
  -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = B ;
• sets Dtran[C, a] = B;
• computes -closure(move(C, b)) = -closure(move({1, 2, 4, 5, 6, 7}, b)) =
  -closure({5}) = {1, 2, 4, 5, 6, 7} = C;
• sets Dtran[C, b] = C.

The fourth iteration of the while-loop:

• marks D;
• computes -closure(move(D, a)) = -closure(move({1, 2, 4, 5, 6, 7, 9}, a)) =
  -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = B ;
• sets Dtran[D, a] = B;
• computes -closure(move(D, b)) = -closure(move({1, 2, 4, 5, 6, 7, 9}, b)) =
  -closure({5, 10}) = {1, 2, 4, 5, 6, 7, 10};
• enters E = {1, 2, 4, 5, 6, 7, 10} as an unmarked state in Dstates; and
• sets Dtran[D, b] = E.

The fifth iteration of the while-loop:

• marks E;
• computes -closure(move(E, a)) = -closure(move({1, 2, 4, 5, 6, 7, 10}, a)) =
  -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = B ;
• sets Dtran[E, a] = B;
• computes -closure(move(E, b)) = -closure(move({1, 2, 4, 5, 6, 7, 10}, b)) =
  -closure({5}) = {1, 2, 4, 5, 6, 7} = C;
• sets Dtran[E, b] = C.

All five states in Dstates are now marked so the Subset Construction algorithm is done. The resultant DFA is shown in Figure 3.29.

This section shows Thompson's Construction Algorithm for constructing an NFA from a regular expression. One can then use the subset construction algorithm in section 3.6 to construct a DFA which can then be easily simulated to obtain a recognizer for the regular expression.

Construction of an NFA from a Regular Expression: The construction is guided by the syntax of the regular expression with cases following the cases in the definition of a regular expression. From section 3.3, the definition of a regular expression is:

1. is a regular expression that denotes {}, the set containing just the empty string.

2. If a is a symbol in the alphabet then the regular expression a denotes {a}, the set containing just that symbol.

3. Suppose s and t are regular expressions denoting languages L(s ) and L(t ), respectively. Then:

   a): (s ) | (t ) is a regular expression denoting L(s ) |_| L(t );
   b): (s )(t ) is a regular expression denoting L(s )L(t );
   c): (s )* is a regular expression denoting L(s )*; and
   d): (s ) is another regular expression denoting L(s ).

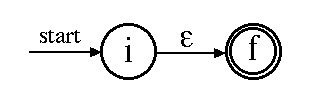
Case 1:

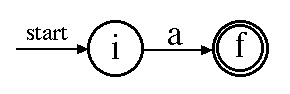
Case 2: a

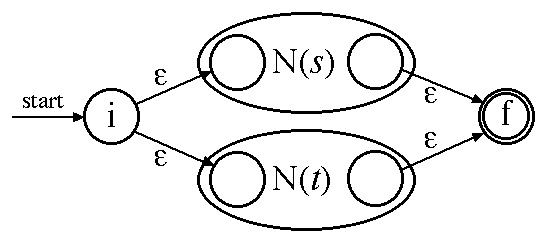
Case 3a: (s ) | (t )

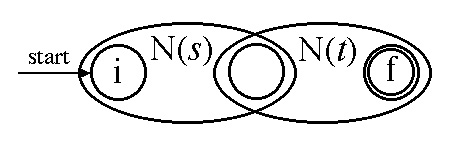
Case 3b: (s )(t )

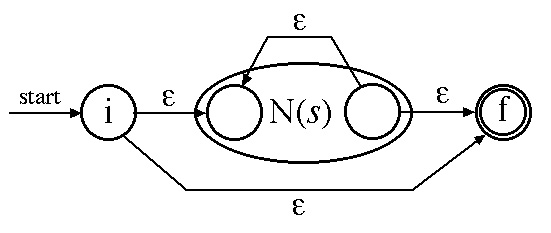
Case 3c: (s )*

Example 3.16 in the text illustrates Thompson's construction algorithm for the regular expression: ( a | b )*a b b - the regular expression is parsed as shown in Figure 3.30 and Figure 3.27 shows the resultant NFA.